全排列递归算法(Python实现)
目录
概述
本文由浅入深,由特殊到一般说明全排列的递归实现。
需求
编写程序,输出所有由a,b,c,d四个字母都出现一次所组成的字符串。
分析
这实际是全排列问题,一共有 4! = 24 个结果。
暴力穷举
思路:和解数学题一样,第一位从四个字母中选择,有4种可能,第二位从剩余3个字母中选择,有3种可能,依此类推,第三位2种,第四位1种。
result = [] # 保存全排列结果
for a in ('abcd'):
for b in ('abcd'.replace(a,'')):
for c in ('abcd').replace(a,'').replace(b,''):
for d in ('abcd').replace(a,'').replace(b,'').replace(c,''):
result.append(f'{a}{b}{c}{d}') # f-string,python 3.6 支持的语法
for x in result:
print(x)
上述代码虽然实现了需求,但局限也很明显,如果给的字母个数有变,程序需要调整,如果字母个数非常多,程序将变得难以阅读,无法维护,所以以上代码只能算临时代码,无法复用,不能"投产"。
递归实现
字符串
思路:abcd的全排列,等于 a + bcd的全排列,b + acd的全排列,c + abd的全排列,d + abc的全排列。显然,从以上描述就可看出问题具有递归性质。
实现:依次取出一个字母作为前缀加入到当前结果字符串,剩余字母再全排列,直至只剩余最后一个字母。
def permutation_sub(prefix_str,suffix_str,result):
if len(suffix_str) == 0: # 当后缀为空时,即产生一个结果
result.append(prefix_str)
for s in suffix_str:
permutation_sub(prefix_str + s, suffix_str.replace(s,''), result)
def permutation(input_str):
perm = []
permutation_sub('',input_str,perm)
return perm
if __name__ == "__main__":
for x in permutation('abcd'):
print(x)
运行结果正确。
列表
错误写法
以上写法仅合适字符串的场景,更一般的场景用列表作为输入。那我们用列表模仿以上过程:
def permutation_sub(prefix_ls,suffix_ls,result):
if len(suffix_ls) == 0:
result.append(list(prefix_ls))
return
for x in suffix_ls:
prefix_ls.append(x)
suffix_ls.remove(x)
permutation_sub(prefix_ls ,suffix_ls ,result)
def permutation(input_ls):
perm = []
permutation_sub([],input_ls,perm)
return perm
if __name__ == "__main__":
for x in permutation(['a','b','c','d']):
print(x)
运行结果错误。因为list在python中是可变类型,不像str是非可变类型,每次操作都会产生一个新对象,list参数传的是一个地址,后续不断的递归调用过程中list内容全一直改变,所以上述写法不适合list参数。
正确写法
解决方案是用元素交换来模拟上述字符新加与移除的过程,思路是从下标0开始,依次选择后续元素与领导元素(第0个元素)交换,作为新的领导元素,递归以上过程,直到下标达到最大。
def permutation_sub(ls,start,result):
if start == len(ls) - 1:
result.append(list(ls))
return
for i in range(start,len(ls)):
ls[i],ls[start] = ls[start],ls[i] # 后续元素依次与start交换,作为领导元素
permutation_sub(ls,start + 1,result)
ls[i],ls[start] = ls[start],ls[i] # 再次交换,复原上次结构,方便进行下个元素的交换
def permutation(ls):
perm = []
permutation_sub(ls,0,perm)
return perm
if __name__ == "__main__":
for x in permutation(['a','b','c','d']):
print(x)
以上代码有两个细节:
- 第3行的list(ls),相当于copy.copy(ls),表示复制元素构建一个新的列表,否则最后保存的都是相同的list
- 第8行有个再次交换的过程,方便回溯前还原上次调用前的列表元素结构,进行下次调用(i + 1)
过程图解
以a,b,c作为输入的图解
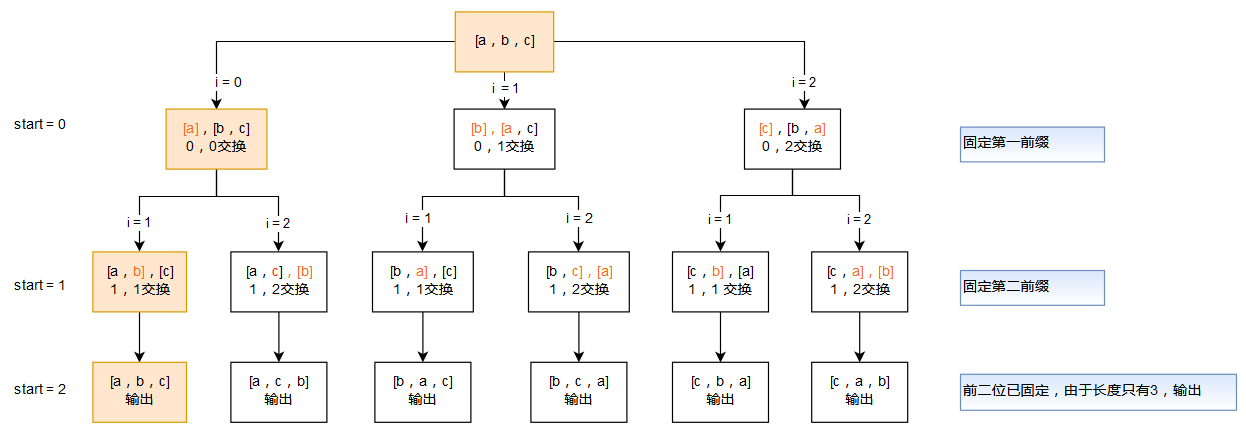
执行顺序类似一个N叉树深度优先的遍历过程(左边黄色部分从上到下为第一轮输出的执行顺序),递归每向下一层就确定了一个新的前缀,每次向上回溯前都要再次交换还原上次列表状态。